No products in the cart.
Pravděpodobnostní grafické modely
Prerekvizity
- Základní znalost programování v Pythonu
- Středoškolské znalosti lineární algebry, matematické analýzy a teorie pravděpodobnosti. Bude předpokládáno základní porozumění pojmům jako vektor, matice, vektorový prostor, pravděpodobnost, podmíněná pravděpodobnost, nezávislost náhodných jevů a znalost násobení matic a derivace funkcí.
Co si účastník odnese
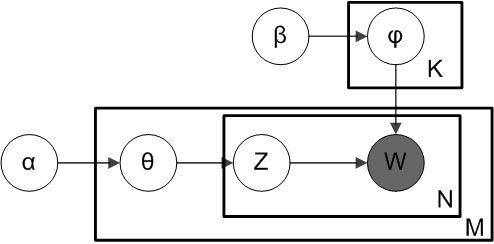
Tento kurz je určen pro zájemce o porozumění Bayesovským sítím a pravděpodobnostnímu programování. Teoretická příprava v první části kurzu bude směřovat k praktickému příkladu modelování témat pomocí Latent Dirichlet Allocation a jejímu neparametrickému rozšíření včetně odhadu hyperparametrů. Po absolvování kurzu bude účastník schopen navrhovat a implementovat vlastní jednoduché Bayesovské sítě pro různé problémy.
Osnova
- Bayesovské sítě
- Grafická reprezentace modelu
- Generativní vs. diskriminativní modely
- Statistická inference v Bayesovských sítích
- Variational inference
- Sampling
- Rejection sampling
- Markov Chain Monte Carlo
- Metropolis-Hastings sampling
- Gibbs sampling
- Pravděpodobnostní rozdělení
- Binomické a multinomické rozdělení
- Beta a Dirichletovo rozdělení
- Gamma rozdělení
- Pravděpodobnostní programovací jazyky
- Praktický příklad na modelování témat
- Latent Semantic Analysis
- Probabilistic Latent Semantic Analysis
- Latent Dirichlet Allocation
- Neparametrické modely
- Dirichlet process
- Chinese restaurant process a Stick breaking process
- Non-parametric LDA
- Odhad hyperparametrů