Data sama o sobě by nebyla příliš užitečná, pokud bychom z nich nebyli schopni vyvozovat závěry a ty následně využívat. Interpretace dat však není jednoduchá disciplína a často dochází k tomu, že jsou data omylem, nebo dokonce záměrně, interpretována chybně. Na nejčastější problémy, které při interpretaci dat způsobují problémy se podíváme blíže.

Nedostatečná reprezentativita data

Jestliže máme pro popis zkoumaného jevu málo dat a data daný jev nereprezentují dostatečně, říkáme, že data nejsou reprezentativní.  Aby byla data reprezentativní, je třeba mít vzorek co největší a správně vybraný. Příkladem nereprezentativních dat je náš vzorek mezd deseti lidí z předchozí kapitoly. Deset příkladů není dostatečné množství, které by reprezentovalo distribuci mezd v České republice ani její základní charakteristiky.

Šum v datech

Šumem rozumíme náhodnou chybu, která ovlivňuje data. V datech se téměř vždy nějaký šum vyskytuje a pokud není příliš velký, tak nám nevadí. Náhodné odchylky dat od skutečnosti se totiž při dostatečné velikosti dat “vynulují” a statistiky tak příliš neovlivní. Příklad takového šumu vidíme na obrázku 1. Skutečně naměřená veličina je zde zobrazena modrou křivkou. Aplikací jednoduchých matematických metod dokážeme náhodné odchylky částečně eliminovat a dostaneme tak červenou křivku.

Obrázek 1. Šum v datech a jeho vyhlazení.

Bias v datech

Bias (někdy v češtině označovaný jako podjatost) je systematická chyba, která ovlivňuje data. Tento druh chyby nám vadí, protože může výrazně ovlivňovat globální statistiky jako průměr, medián a další.  Bias může být způsobený i nevhodným výběrem vzorku dat (výběrové zkreslení).

Příkladem může být situace, kdy bychom do dat pro určení statistik o mzdách v České republice vybrali pouze absolventy vysokých škol žijící v Praze. Vzhledem k tomu, že absolventi vysokých škol v Praze mají v porovnání se zbytkem republiky nadprůměrné mzdy, byly by statistiky nadhodnoceny.

Změny podmínek při sběru dat

Některé veličiny a ukazatele (například průměrná mzda) se vyvíjí v čase. Nemůžeme tedy například sbírat data o mzdách v roce 2010 a dělat z nich závěry o mzdách v roce 2021. Vývoj mezd v České republice od roku 2000 do roku 2018 ilustruje graf na obrázku 2.

Obrázek 2: Vývoj mezd v České republice v období let 2000 až 2018.

Korelace a kauzalita

Korelace vyjadřuje míru závislosti mezi dvěma veličinami. Například četnosti výskytů slimáků a žížal na zahrádce spolu silně korelují. Pokud najdeme velké množství žížal, máme velkou šanci najít velké množství slimáků a naopak.

Kauzalita je vztahem dvou veličin, kde hodnota jedné přímo ovlivňuje hodnotu druhé. Příčinou zvýšeného výskytu slimáků a žížal je většinou deštivé počasí. Zvýšený výskyt slimáků sám o sobě zvýšený výskyt žížal nezpůsobuje. Stejně tak zvýšený výskyt žížal nezpůsobuje zvýšený výskyt slimáků.

Rozdíl mezi korelací a kauzalitou na příkladu žížal a slimáků je schematicky znázorněn na obrázku 3.

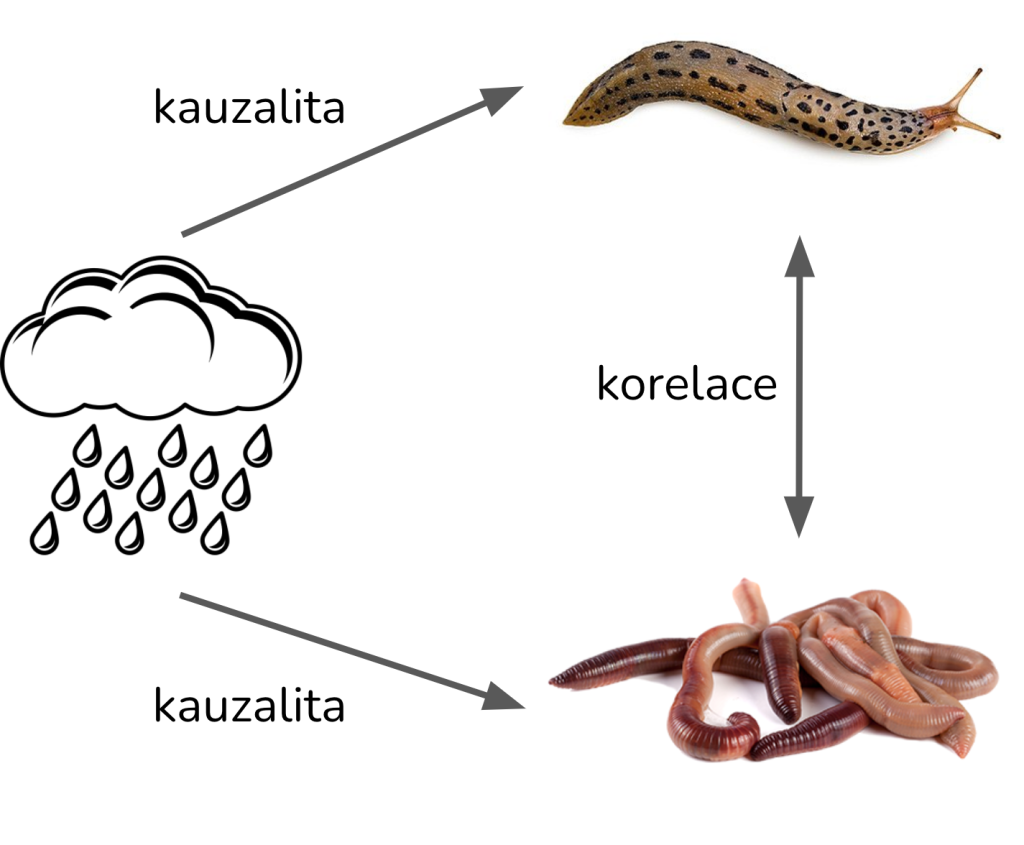
Obrázek 3: Ilustrace rozdílu mezi korelací a kauzalitou. Výskyty žížal a výskyty slimáků na zahrádce spolu silně korelují. Oba jevy jsou ale způsobeny deštivým počasím.

V praxi je někdy obtížné odlišit korelaci a kauzalitu. Je to však nesmírně důležité. Dlouho například nebylo prokázáno, že kouření způsobuje rakovinu, přestože bylo jasné, že tyto dva jevy spolu korelují.