Data jsou typicky příliš velká na to, aby je člověk dokázal interpretovat přímo. Pro porozumění datům je tedy třeba používat různé matematické nástroje. Pro základní popis dat slouží takzvaná popisná statistika, na jejíž nejdůležitější nástroje se v této kapitole podíváme blíže.

Střední hodnota (aritmetický průměr)

Střední hodnota je základní statistický ukazatel, který je v případě diskrétních dat roven aritmetickému průměru. V takovém případě ho snadno spočítáme jako:

Pro ilustraci si zvolme konkrétní vzorek dat

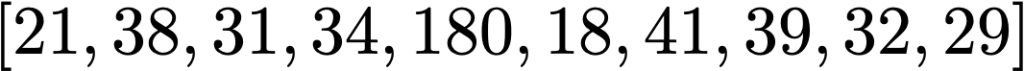
Jedná se o měsíční mzdy v tisících korunách malé náhodné skupiny lidí v ČR v roce 2021. Konkrétní výpočet průměrné mzdy bude vypadat následovně:

Tento konkrétní příklad pěkně ilustruje problém použití střední hodnoty jako jediného ukazatele pro posouzení výše mezd ve skupině lidí. Rozdělení mezd ve společnosti totiž není symetrické. Typicky má velké množství lidí mzdy relativně malé a pouze nepatrný zlomek lidí mzdy extrémně vysoké. Právě tyto vysoké hodnoty ale výrazně ovlivňují průměr a posouvají ho k vyšším hodnotám. V našem vzorku je to hodnota 180.

Pro představu se podívejme na distribuci mezd v České republice za rok 2020. Ta je zachycena na obrázku 1. Kdyby byly mzdy rozloženy rovnoměrně, byl by graf symetrický podle svislé osy. Zde je ale jednoznačně vidět, že většina zaměstnanců má měsíční mzdu spíše menší.

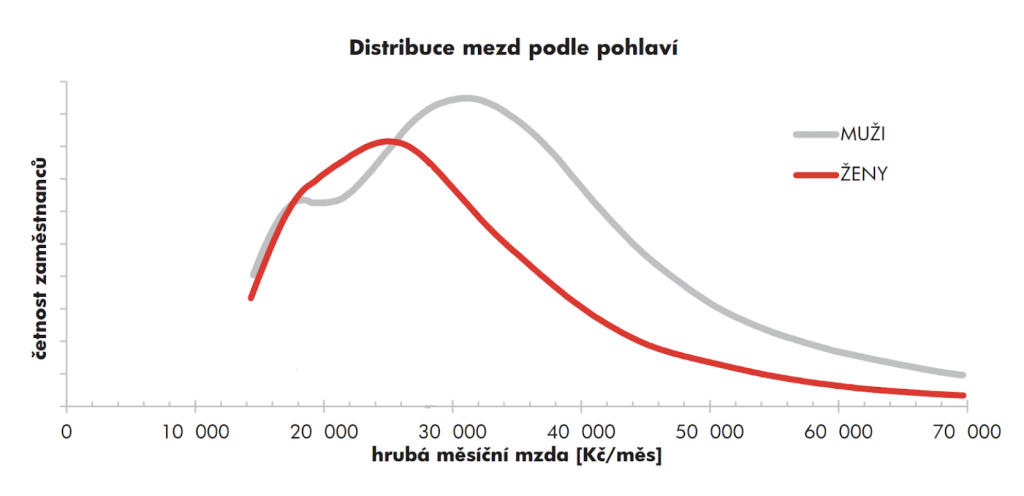
Obrázek 1: Distribuce mezd v ČR podle pohlaví za rok 2020. Zdroj: https://ispv.cz/.

Medián a další kvantily

Řešením výše popsaného problému je použití vhodnějšího statistického ukazatele, kterým v tomto případě může být medián. Medián je hodnota, jež dělí řadu vzestupně seřazených čísel na dvě stejně početné poloviny. V našem případě to bude výše mzdy, pro kterou platí, že počet lidí s menší mzdou je stejný jako počet lidí s vyšší mzdou. Pokud bychom ve zkoumaném vzorku měli sudý počet lidí, medián by byl průměrem dvou prostředních hodnot.

Pokud bychom řadu rozdělili jinde než v polovině, dostaneme další statistické ukazatele, nazývané obecně kvantily. Mezi další nejpoužívanější kvantily patří kvartily (rozdělující data na čtvrtiny), decily (rozdělující data na desetiny) a percentily (rozdělující data na setiny).

Na obrázku 2 vidíme distribuci mezd v České republice za rok 2020, včetně vyznačeného průměru a nejdůležitějších kvantilů.

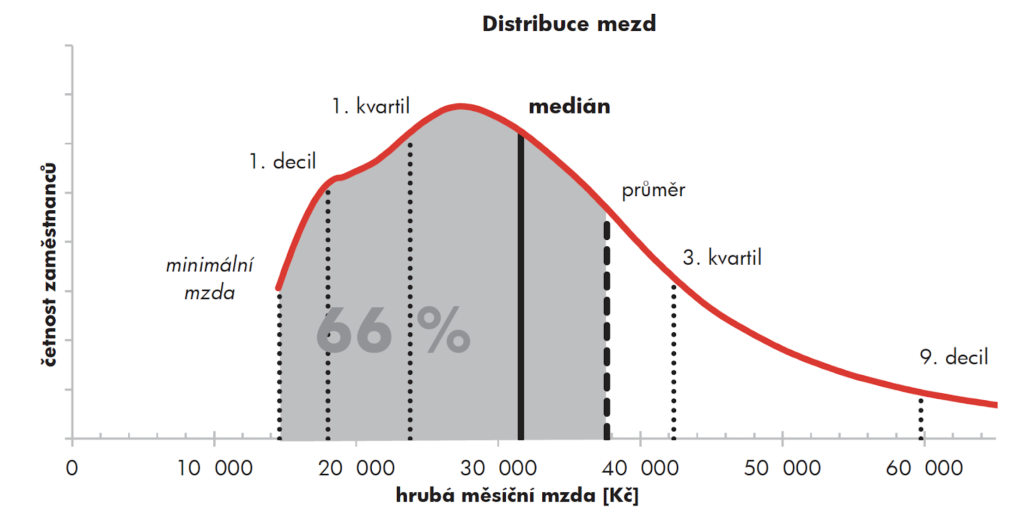
Obrázek 2: Distribuce mezd v ČR podle pohlaví za rok 2020, včetně vyznačeného průměru a nejdůležijějších kvantilů. Zdroj: https://ispv.cz/.

Rozptyl a směrodatná odchylka

Při zkoumání vzorku dat je pro nás důležitou informací také jeho variabilita. Průměrné odchylky od střední hodnoty (aritmetického průměru) zkoumají statistické ukazatele rozptyl a směrodatná odchylka. Rozptyl je definovaný jako kvadrát průměrných odchylek od průměru. Směrodatná odchylka potom jako odmocnina rozptylu. Směrodatná odchylka má oproti rozptylu výhodu v tom, že vychází ve stejných jednotkách jako zkoumaná veličina.

Pro náš vzorek mezd můžeme rozptyl spočítat jako

A směrodatnou odchylku potom jako